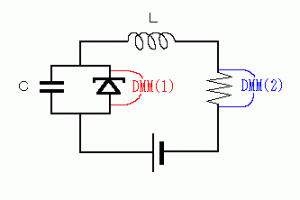
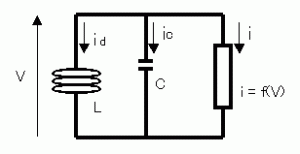
実験で使った回路の等価回路を下の図に示した。トンネルダイオードの静特性を表す部分f(v)は、 静特性で得られたグラフをVの3次関数でフィッティングして、電源電圧V0で与えられる点を原点としたものである。
ここから、次の関係式が得られる。
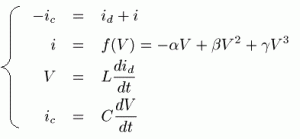
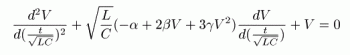
|
物理学実験3 17.トンネルダイオード |
|
2.発振の測定〜Self excited Oscillation〜
|
|
発振現象を回路方程式を用いて定量的に考えてみる。 実験で使った回路の等価回路を下の図に示した。トンネルダイオードの静特性を表す部分f(v)は、 静特性で得られたグラフをVの3次関数でフィッティングして、電源電圧V0で与えられる点を原点としたものである。 ここから、次の関係式が得られる。 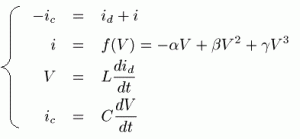
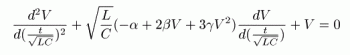
|
  |
|
|
これはSelf-ecxited oscillationを記述する「van der Pol equation」として知られている。 これは非線形の微分方程式なので一般に正確には解けない。そこで数値計算によってとく事になるが、 そのときに扱いやすいように無次元化しておく。 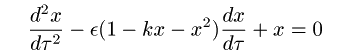
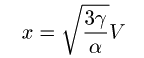
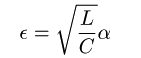
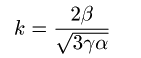
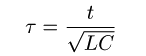
・Javaによるシミュレーション この方程式をRunge-Kutta法によって解き、結果を描くアプレットを製作した。 実験結果の「L=8.9[μH],C=11.1[nF]」のとき、イプシロンの値は1.91である。 実験結果に近いシミュレーションが得られた。 また、イプシロンが大きくなっていくにしたがって、電圧のジャンプがすばやく(?)なっている事も分かる。 これも実験結果に一致する。V−tグラフを見ても分かるように、急激な変化をするグラフになるので 数値計算の刻み幅を小さくしないと微係数が無限大に発散してしまい正確な計算ができない。 アプレットでは計算回数を制限しているためイプシロンは10までしかあげられないようになっている。 しかし、ジャンプが急激になっていく様子は確認できると思う。 これらの事から発振が起こる原因として一番重要なのは「トンネルダイオードの静特性が負性抵抗領域(Negative Registance) を持つことである」という事が分かった。 |